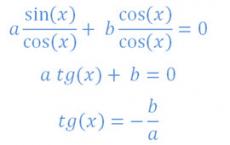Уравнение с косинусом и дробью. Более сложные тригонометрические уравнения
Урок и презентация на тему: "Решение простейших тригонометрических уравнений"
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине "Интеграл" для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Программная среда "1С: Математический конструктор 6.1"
Что будем изучать:
1. Что такое тригонометрические уравнения?
3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.
Что такое тригонометрические уравнения?
Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс. Теперь давайте посмотрим на тригонометрические уравнения в общем.
Тригонометрические уравнения – уравнения в котором переменная содержится под знаком тригонометрической функции.
Повторим вид решения простейших тригонометрических уравнений:
1)Если |а|≤ 1, то уравнение cos(x) = a имеет решение:
X= ± arccos(a) + 2πk
2) Если |а|≤ 1, то уравнение sin(x) = a имеет решение:
3) Если |а| > 1, то уравнение sin(x) = a и cos(x) = a не имеют решений 4) Уравнение tg(x)=a имеет решение: x=arctg(a)+ πk
5) Уравнение ctg(x)=a имеет решение: x=arcctg(a)+ πk
Для всех формул k- целое число
Простейшие тригонометрические уравнения имеют вид: Т(kx+m)=a, T- какая либо тригонометрическая функция.
Пример.Решить уравнения: а) sin(3x)= √3/2
Решение:
А) Обозначим 3x=t, тогда наше уравнение перепишем в виде:
Решение этого уравнения будет: t=((-1)^n)arcsin(√3 /2)+ πn.
Из таблицы значений получаем: t=((-1)^n)×π/3+ πn.
Вернемся к нашей переменной: 3x =((-1)^n)×π/3+ πn,
Тогда x= ((-1)^n)×π/9+ πn/3
Ответ: x= ((-1)^n)×π/9+ πn/3, где n-целое число. (-1)^n – минус один в степени n.
Ещё примеры тригонометрических уравнений.
Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3Решение:
А) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:
X/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk
Ответ: x=5πk, где k – целое число.
Б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3
3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3
Ответ: x=2π/9 + πk/3, где k – целое число.
Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке .
Решение:
Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk
4x= ± π/4 + 2πk;
X= ± π/16+ πk/2;
Теперь давайте посмотрим какие корни попадут на наш отрезок. При k
При k=0, x= π/16, мы попали в заданный отрезок .
При к=1, x= π/16+ π/2=9π/16, опять попали.
При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать.
Ответ: x= π/16, x= 9π/16
Два основных метода решения.
Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.Решим уравнение:
Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).
В результате замены получим: t 2 + 2t -1 = 0
Найдем корни квадратного уравнения: t=-1 и t=1/3
Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.
X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.
Ответ: x= -π/4+πk; x=arctg(1/3) + πk.
Пример решения уравнения
Решить уравнений: 2sin 2 (x) + 3 cos(x) = 0
Решение:
Воспользуемся тождеством: sin 2 (x) + cos 2 (x)=1
Наше уравнение примет вид:2-2cos 2 (x) + 3 cos (x) = 0
2 cos 2 (x) - 3 cos(x) -2 = 0
Введем замену t=cos(x): 2t 2 -3t - 2 = 0
Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2
Тогда cos(x)=2 и cos(x)=-1/2.
Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.
Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Ответ: x= ±2π/3 + 2πk
Однородные тригонометрические уравнения.
Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени.Уравнения вида
однородными тригонометрическими уравнениями второй степени.
Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x):
 Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.
Решить уравнение:
Пример: cos 2 (x) + sin(x) cos(x) = 0
Решение:
Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0
Тогда нам надо решить два уравнения:
Cos(x)=0 и cos(x)+sin(x)=0
Cos(x)=0 при x= π/2 + πk;
Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):
1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk
Ответ: x= π/2 + πk и x= -π/4+πk
Как решать однородные тригонометрические уравнения второй степени?
Ребята, придерживайтесь этих правил всегда!
1. Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:

Делаем замену переменной t=tg(x) получаем уравнение:
Решить пример №:3
Решить уравнение:Решение:
Разделим обе части уравнения на косинус квадрат:
Делаем замену переменной t=tg(x): t 2 + 2 t - 3 = 0
Найдем корни квадратного уравнения: t=-3 и t=1
Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk
Tg(x)=1 => x= π/4+ πk
Ответ: x=-arctg(3) + πk и x= π/4+ πk
Решить пример №:4
Решить уравнение:Решение:
Преобразуем наше выражение:

Решать такие уравнение мы умеем: x= - π/4 + 2πk и x=5π/4 + 2πk
Ответ: x= - π/4 + 2πk и x=5π/4 + 2πk
Решить пример №:5
Решить уравнение:Решение:
Преобразуем наше выражение:

Введем замену tg(2x)=t:2 2 - 5t + 2 = 0
Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2
Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2
2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2
Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2
Задачи для самостоятельного решения.
1) Решить уравнениеА) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7
2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].
3) Решить уравнение: ctg 2 (x) + 2ctg(x) + 1 =0
4) Решить уравнение: 3 sin 2 (x) + √3sin (x) cos(x) = 0
5) Решить уравнение:3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0
6)Решить уравнение:cos 2 (2x) -1 - cos(x) =√3/2 -sin 2 (2x)
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х - угол, который нужно найти,
а - любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло...) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда. При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = - arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания "С" будут по плечу. С неравенствами, с отбором корней из заданного интервала... Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли...)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6. Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) - одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4...) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это... того... из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, - 1; 0; √3; 1/2; √3/2 и т.п. - ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да...) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово - два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там - два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Если Вам нравится этот сайт...
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)
можно познакомиться с функциями и производными.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Не секрет, что успех или неудача в процессе решения практически любой задачи, в основном зависит от правильности определения типа заданного уравнения, а также от правильности воспроизведения последовательности всех этапов его решения. Однако в случае с тригонометрическими уравнениями, определить факт того, что уравнение именно тригонометрическое, вовсе несложно. А вот в процессе определения последовательности действий, которые должны привести нас к правильному ответу, можно столкнуться с определенными сложностями. Давайте разберемся, как решать тригонометрические уравнения правильно с самого начала.
Решение тригонометрических уравнений
Для того, чтобы решить тригонометрическое уравнение, нужно попробовать выполнить следующие моменты:
- Приводим все функции, которые входят в наше уравнение к «одинаковым углам»;
- Нужно довести заданное уравнение до «одинаковых функций»;
- Раскладываем левую часть заданного уравнения на множители или другие нужные составляющие.
Методы
Метод 1. Решать такие уравнения необходимо в два этапа. Первый- преобразовываем уравнение для того, чтобы получить его простейший (упрощенный) вид. Уравнение: Cosx = a, Sinx = a и подобные, называются простейшими тригонометрическими уравнениями. Второй этап- решаем полученное простейшее уравнение. Следует отметить, что простейшее уравнение можно решить алгебраическим методом, который отлично известен нам из школьного курса алгебры. Его также называют методом замены подстановки и переменной. С помощью формул приведения, сначала нужно преобразовать, затем сделать замену и после этого найти корни.
Далее нужно разложить наше уравнение на возможные множители, для этого необходимо перенести все члены влево и затем можно раскладывать на множители. Теперь нужно привести данное уравнение к однородному, в котором все члены равняются одной степени, а косинус и синус имеют один и тот же угол.
Перед тем, как решать тригонометрические уравнения, нужно перенести его члены в левую часть, забрав из правой, а затем выносим все общие знаменатели за скобки. Приравниваем наши скобки и множители к нулю. Наши приравненные скобки представляют собой однородное уравнение с уменьшенной степенью, которое нужно разделить на sin (cos) в старшей степени. Теперь решаем алгебраическое уравнение, которое было получено, в соотношении к tan.
Метод 2. Еще одним методом, с помощью которого, можно решить тригонометрическое уравнение является переход к половинному углу. К примеру, решаем уравнение: 3sinx-5cosx=7.
Нам нужно перейти к половинному углу, в нашем случае это: 6sin(x/2)*cos(x/2)- 5cos²(x/2)+5sin²(x/2) = 7sin²(x/2)+7cos²(x/2).А после этого, сводим все члены в одну часть (для удобства лучше выбрать правую) и приступаем к решению уравнения.
При необходимости можно вводить вспомогательный угол. Это делается в случае, когда нужно заменить целое значение sin (a) или cos (a) и знак «a» как раз и выступает вспомогательным углом.
Произведение в сумму
Как решать тригонометрические уравнения, используя произведение в сумму? Метод известный как преобразование произведения в сумму также может быть использован в решении таких уравнений. В этом случае необходимо использовать соответствующие уравнению формулы.
К примеру, у нас есть уравнение: 2sinx * sin3x= сos4x
Нам нужно решить эту задачу путем преобразования левой части в сумму, а именно:
сos 4x –cos8x=cos4x ,
х = p/16 + pk/8.
Если вышеприведенные методы не подходят, и Вы все еще не знаете, как решать простейшие тригонометрические уравнения, можно воспользоваться еще одним методом – универсальная подстановка. С его помощью можно преобразовать выражение и произвести замену. К примеру: Cos(x/2)=u. Теперь можно решать уравнение с имеющимся параметром u. А получив нужный результат, не забываем перевести это значение в обратное.
Многие «опытные» ученики советуют обратиться за решением уравнений к людям в онлайн-режиме. Как решить тригонометрическое уравнение онлайн, спросите Вы. Для онлайн решения задачи, Вы можете обратиться на форумы соответствующей тематике, где Вам могут помочь советом или же в решении задачи. Но лучше всего, все же попытаться обойтись собственными силами.
Навыки и умения в решении тригонометрических уравнений являются очень важными и полезными. Их развитие потребует от Вас немалых усилий. С решением таких уравнений связаны многие задачи физики, стереометрии и т.д. А сам процесс решения подобных задач предполагает собой наличие умений и знаний, которые можно приобрести во время изучения элементов тригонометрии.
Учим тригонометрические формулы
В процессе решения уравнения Вы можете столкнуться с надобностью использования любой формулы из тригонометрии. Можно, конечно, начать искать ее в своих учебниках и шпаргалках. А если эти формулы отложены у Вас в голове, вы не только сэкономите свои нервы, но и значительно облегчите себе задачу, не тратя времени на поиск нужной информации. Таким образом, у Вас будет возможность для продумывания наиболее рационального пути решения поставленной задачи.